set
约 9129 字大约 30 分钟
2025-06-21
C++ 主要分为两种容器,一种是 vector、list 这类的序列式容器,主要存储数据。另一种是 map、set 这类关联式容器,目的不单纯是为了存储,"关联" 是指通过键来关联和访问容器中的元素。
1.set 简介
template<
class Key,
class Compare = std::less<Key>,
class Allocator = std::allocator<Key>
> class set;set 是 C++ 的容器,底层使用了平衡搜索树的红黑树(Red-Black Tree)。这里我给一份 set 接口文档 供您参考,其他容器差不多,使用起来很简单。
由于二叉树的性质,导致这个容器有以下的特点:
不能直接插入有重复的元素,这是定义导致的,一旦这么做就会插入失败,但是代码不会报错,只会返回一个键值对
std::pair<iterator, bool>,内部是一个迭代器类型和布尔类型,返回的键值对中布尔值被设置为false补充:
pair实际就是一个类,可以存储两个值,一个叫key值,一个叫value值,一个pair对象就可以管理一对键值对,这很有用,这里给您一个 pair 类说明文档 供您参考,您可前去一看。不允许通过迭代器直接修改元素,这会导致搜索树的结构被破坏
合理使用迭代器时,该容器可以达到排序和去重的目的(实际上是走了一个中序遍历)
set的删除接口erase()有时不直接返回真和假,而是返回元素个数,这是为了和multiset同步
补充:除了
set以外还有一个multiset,是一颗允许插入键值冗余的平衡搜索二叉树,使用这个容器可以达到排序的目的。其他的功能和set差不多,但是使用count()接口的时候会出现些许不同(返回一个键值的出现次数),而使用find()会按照中序的顺序查找,同样这里我也给出一份 map 接口文档 供您参考。template< class Key, class Compare = std::less<Key>, class Allocator = std::allocator<Key> > class multiset;
2.map 简介
template<
class Key,
class T,
class Compare = std::less<Key>,
class Allocator = std::allocator<std::pair<const Key, T>>
> class map;而 map 是存储键值对的关联容器,依靠 pair<Key, T> 键值对结构对象来构造二叉树(或者使用函数模板 make_pair() 的自动推导和构造,而且一般是作为内联),底层也是红黑树,这里我依旧给了一份 接口文档。
其中
find()函数的返回值是一个迭代器,指向要查找的键值对,如果找到了指定的键,则返回指向该键值对的迭代器(如未找到指定的键,则返回指向map迭代器end())不过
map有个别具一格的[]重载,可以根据key值,查找和修改对应的value值其中
insert()的返回值也很特殊,是一个pair<iterator, bool>类型V& operator[]<const K& key> { pair<iterator, bool> ret = insert(make_pair(key, V()));//插入的时候有两种可能:成功或者失败,成功返回一个 <当前迭代器, true>,失败返回一个<当前迭代器, false> return *(ret.first).second;//解引用取得迭代器所指的结点,然后返回该结点的 value }这就使得
[]有多种可能性:- 通过
key查找对应的value - 修改
key对应的value值 - 插入从未出现过的
key值,默认value=V()
而前面的
set的插入接口也是类似的原理,甚至我们还可以再进一步简化代码:V& operator[]<const K& key> { return *((insert(make_pair(key, V()))).first).second; }因此,如果第一次看到这样的实现,大概会被吓一跳,这种嵌套过多的代码可以借助额外的变量(匿名对象有名化)来增强代码可读性。
- 通过
值得注意的是,map在别的语言中还有一个更加形象的名字:字典,python采用术语“字典”描述这一种数据结构,并且内嵌进自己的默认语法。
补充:同理
map也有一个multimap的版本,这里是 multimap 类说明文档,尤其需要注意的一点是:multimap不支持[]重载,因为对应了多个value,无法确定是哪一个结点。
3.AVL 树
3.1.定义
我们前面提到过,二叉搜索树虽然可以缩短查找的效率,但是有可能会退化为单枝树,导致效率变成 O(n),因此俄罗斯数学家 G.M.Adelson-Velskii 和 E.M.Landis 在 1962 年发明了一种调整方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过 1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。

补充:这里引入平衡因子是比较好理解的,但是有些
AVL实现是不依赖平衡因子的。
在我们的实现里,结点结构体和 AVL 树类的大概框架就是:
#include <iostream>
#include <utility>
#include <cassert>
using namespace std;
namespace limou
{
//1.结点结构体
template <typename Key, typename Value>
struct AVLTreeNode
{
AVLTreeNode<Key, Value>* _left;
AVLTreeNode<Key, Value>* _right;
AVLTreeNode<Key, Value>* _parent;
pair<Key, Value> _kv;
int _bf;
AVLTreeNode(const pair<Key, Value>& kv)
: _left(nullptr)
, _right(nullptr)
, _parentright(nullptr)
, _kv(kv)
, _bf(0)
{}
};
//2.AVLTree类
template <typename Key, typename Value>
class AVLTree
{
typedef AVLTree<Key, Value> Node;
public:
//1.插入
bool Inster(const pair<Key, Value>& kv);
//2.删除
private:
Node* _root = nullptr;
};
}3.2.插入
3.2.1.插入结点
插入的时候,关于更新平衡因子的大逻辑如下(实际上就是搜索二叉树的插入逻辑,但是最后一部分有关平衡因子的代码是 AVL 树新加入的代码):
#include <iostream>
#include <utility>
#include <cassert>
using namespace std;
namespace limou
{
//1.结点结构体
template <typename Key, typename Value>
struct AVLTreeNode
{
AVLTreeNode<Key, Value>* _left;
AVLTreeNode<Key, Value>* _right;
AVLTreeNode<Key, Value>* _parent;
pair<Key, Value> _kv;
int _bf;
AVLTreeNode(const pair<Key, Value>& kv)
: _left(nullptr)
, _right(nullptr)
, _parentright(nullptr)
, _kv(kv)
, _bf(0)
{}
};
//2.AVLTree类
template <typename Key, typename Value>
class AVLTree
{
typedef AVLTree<Key, Value> Node;
public:
bool Inster(const pair<Key, Value>& kv)
{
//1.搜索二叉树插入的部分
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first > kv.first)
{
parent->_left = cur;
}
else//parent->_kv.first < kv.first
{
parent->_right = cur;
}
cur->_parent = parent;
//2.AVL的部分开始
//插入cur后,更新结点的父节点平衡因子:
//if(cur == parent->right)
// parent->_bf++
//else(cur == parent->left)
// parent->_bf--
//然后出现以下情况:
//if(parent->_bf == 1 || parent->_bf == -1),
//{
// 说明父结点原本的平衡因子必为 parent->_bf == 0,
// 就说明插入后父节点的左右子树高度差发生了改变,
// 则要向上持续更新父节点的部分/全部祖先平衡因子
// if(cur == parent->right) parent->_bf++
// else(cur == parent->left) parent->_bf--
// ...
//}
//else if(parent->_bf == 2 || parent->_bf == -2)
//{
// 说明父节点所在的左右子树已经不平衡了,需要旋转
//}
//else
//{
// 原本是parent->_bf == 1 or parent->_bf == -1,
// 而新插入的cur把高度低的子树变高了,这说明:
// 父节点的左右子树变成了绝对平衡(平衡因子==0),无需更新祖先
//}
//由于插入结点会影响自己的部分/全部的祖先,因此我们的结构加上_parent指针
//然后需要注意有可能会更新到根结点去(最差情况)
while (parent)//最差更新到根节点,根结点的父节点为空,就可以停下
{
if (cur == parent->_right)
{
parent = _bf++;
}
else//cur == parent->_left
{
parent = _bf--;
}
if (parent->_bf == 1 || parent->_bf = -1)
{
//继续更新
parent = parent->_parent;
cur = cur->_parent;
}
else if (parent->_bf == 0)
{
break;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
//旋转
}
else
{
assert(false);//留给我们自己调试使用
}
}
return true;
}
private:
Node* _root = nullptr;
};
}这里还缺少一个最重要的环节:旋转,接下来我们仔细分析四种旋转的情况。
3.2.2.旋转结点
由于我们走到 if-else 语句中的 (parent->_bf == 2 || parent->_bf == -2) 了,那么我们下面假设所有情况的插入都会引发调整,进而旋转。
并且需要注意出现不平衡的情况,其高度一定是大于 2 的。
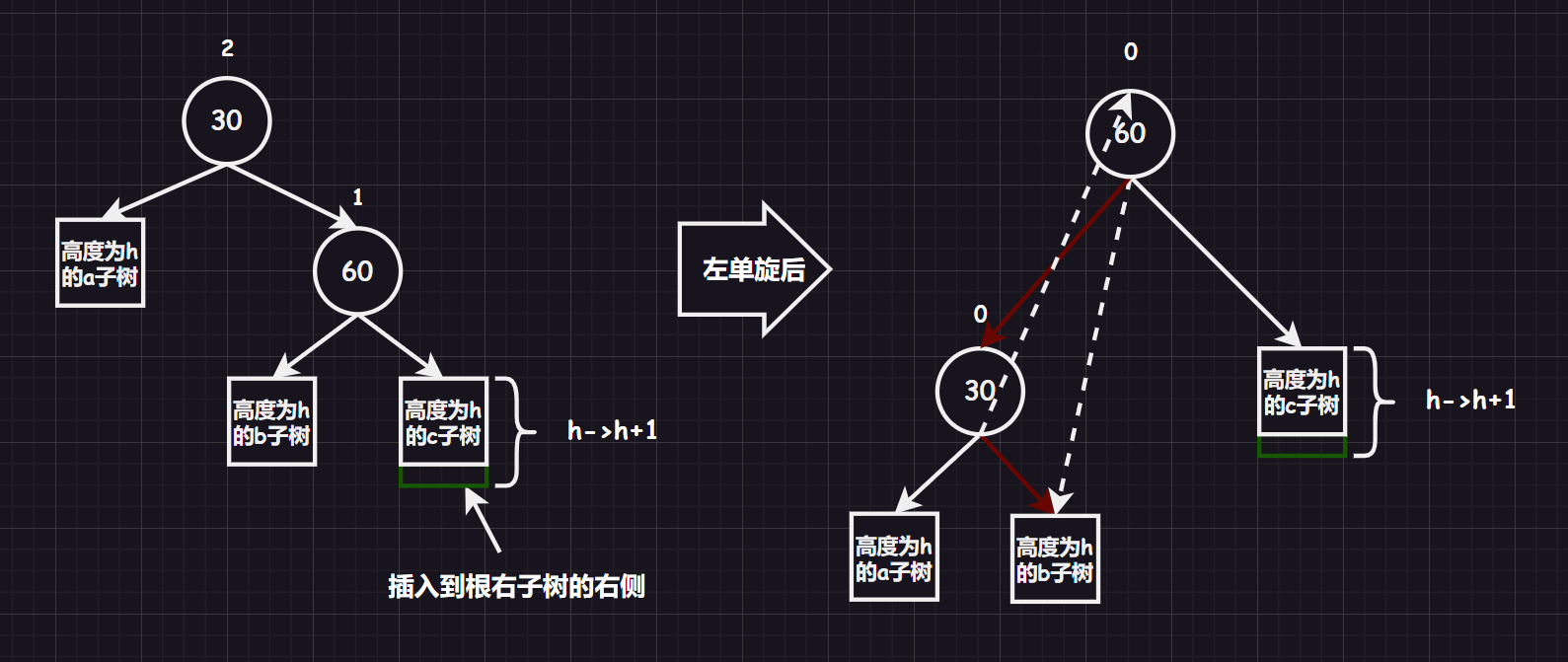
3.2.2.1.左单旋 [新结点插入较高右子树的右侧]
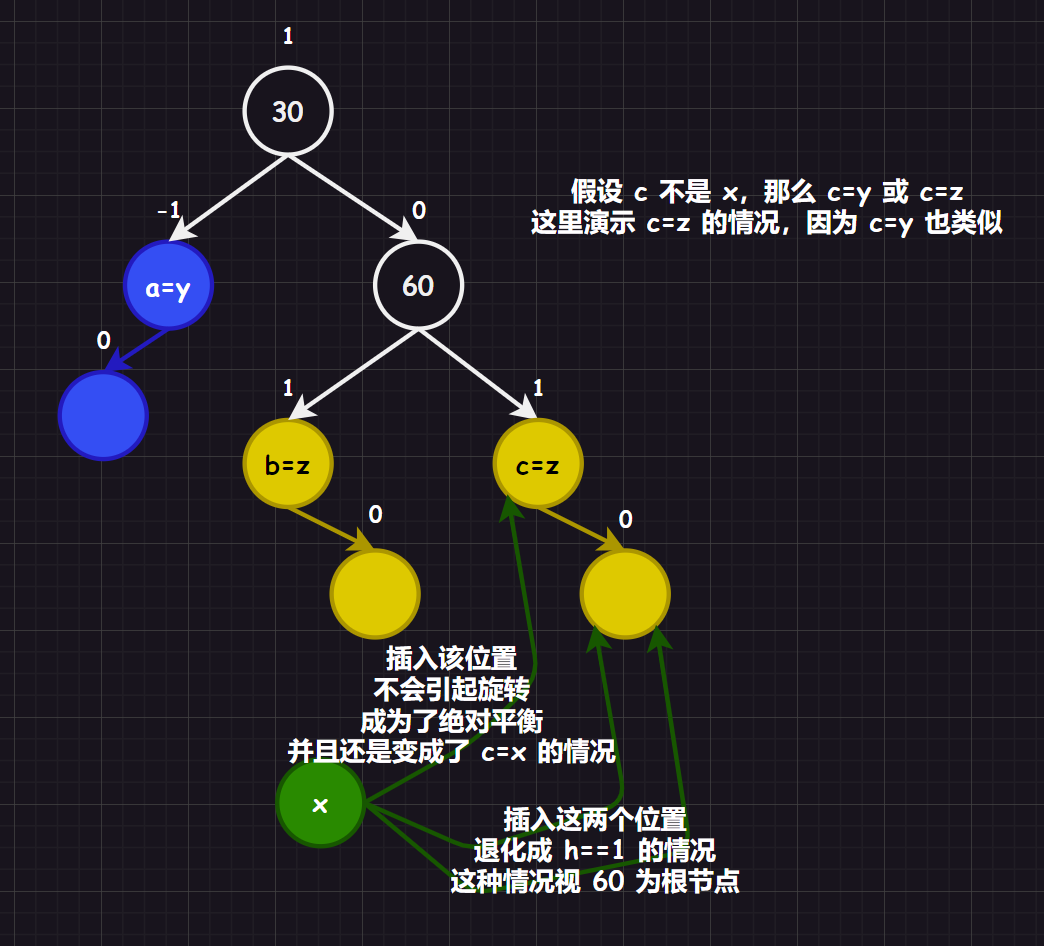
在一颗满足 AVL 树性质的树中,假设根右子树高,将新结点插入到根右子树的右侧。
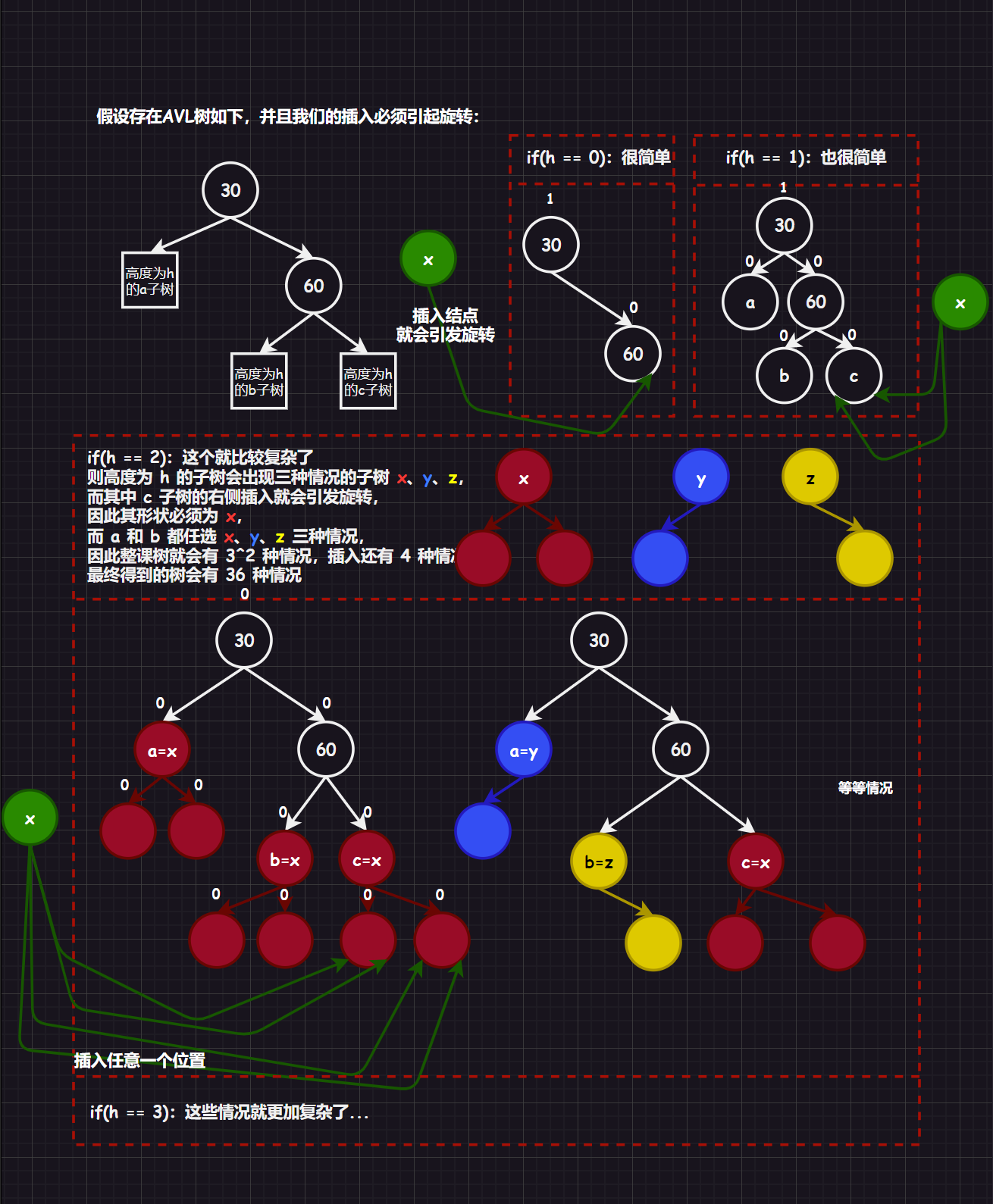
补充:为什么
c必须是x呢?image-20231022104010590
注意:有时间一定要尝试一下
h=4的情况,画一画几个具象树图。
这么一看,插入分析实际上是一件很复杂的事情,但是我们可以通过抽象树图,来简化这一过程。
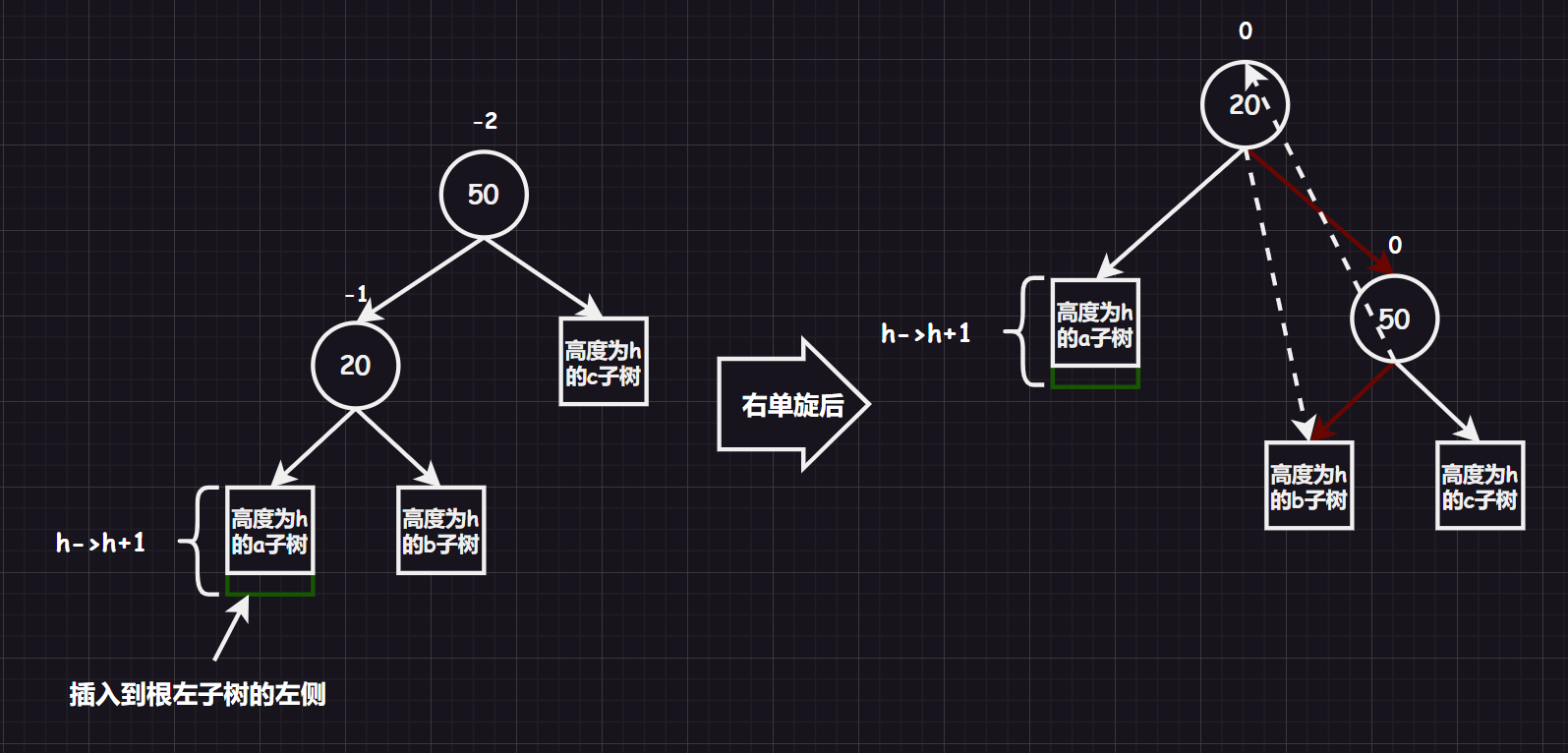
3.2.2.2.右单旋 [新结点插入较高左子树的左侧]
关于右单旋,我们就不画具象树图了(因为和左单旋的情况是镜像的),而是继续采用抽象树图来演示过程:
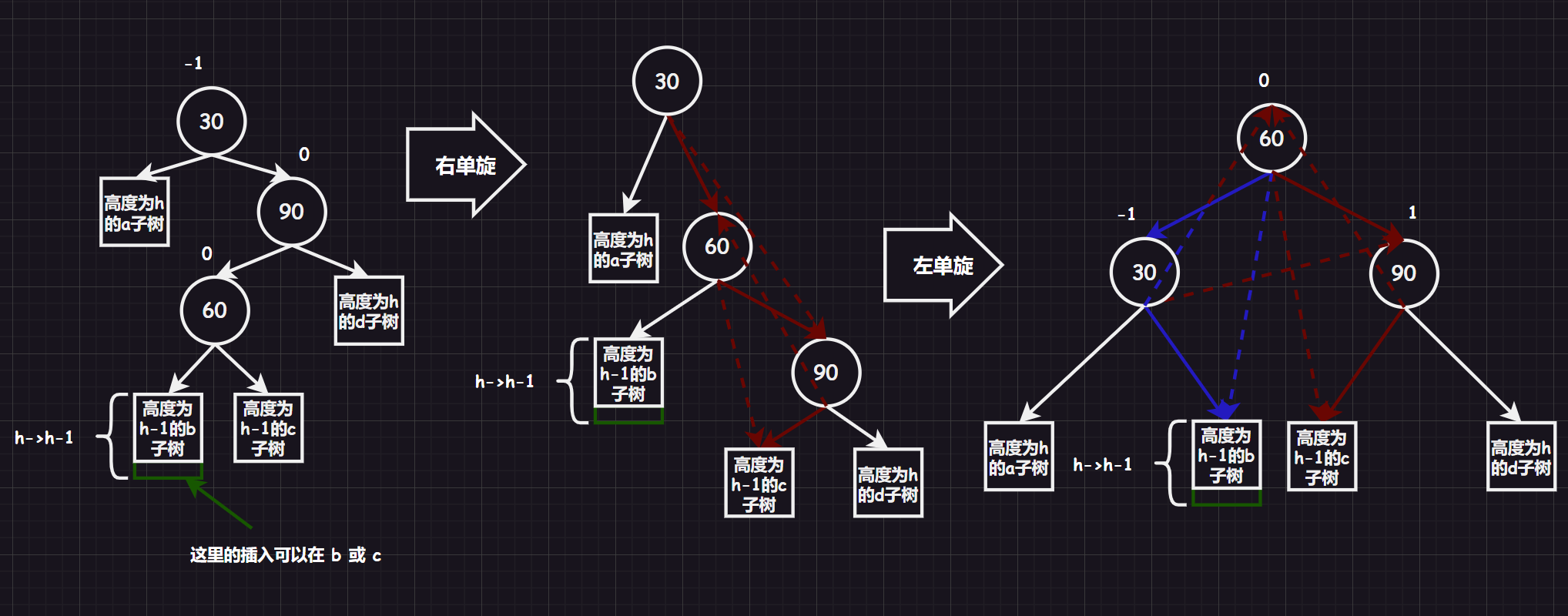
3.2.2.3.先左单旋,再右单旋 [新结点插入较高左子树的右侧]
这里我们也先来分析具象树图,再给出抽象树图旋转的过程。
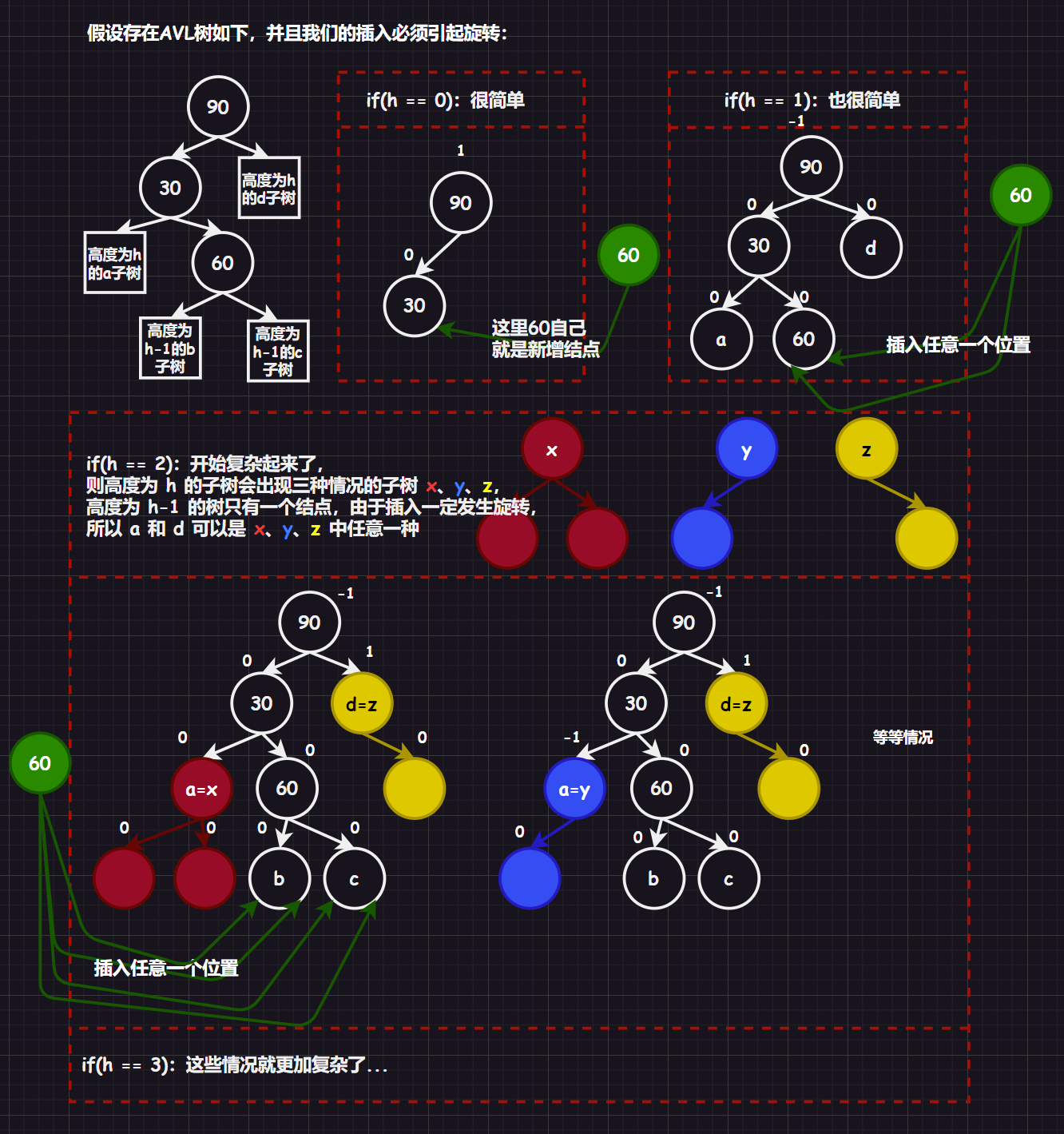
补充:有时间可以试试
h取值为其他的情况。
而抽象树图旋转过程就是:
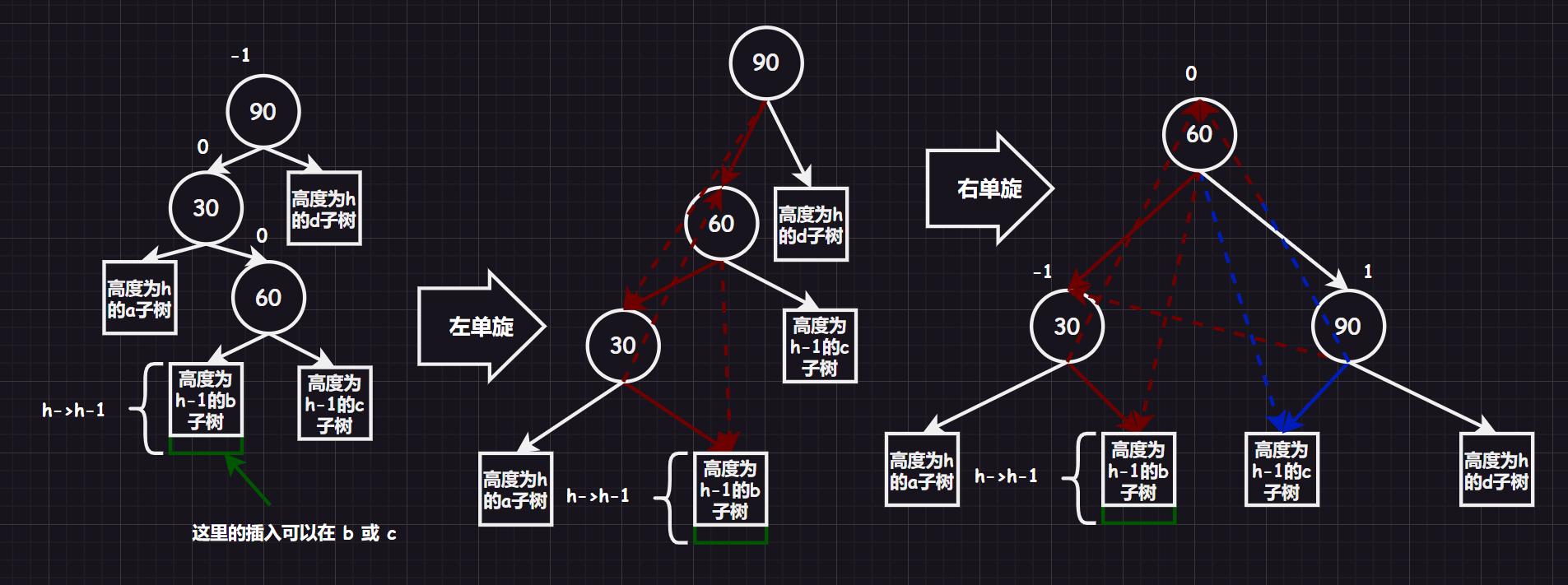
但是在具体代码实现中,最困难的是更新平衡因子的问题(例如:在上图,插入在 b 或者 c 会产生不同的平衡因子)。
让我们来具体分析一下平衡因子的情况:
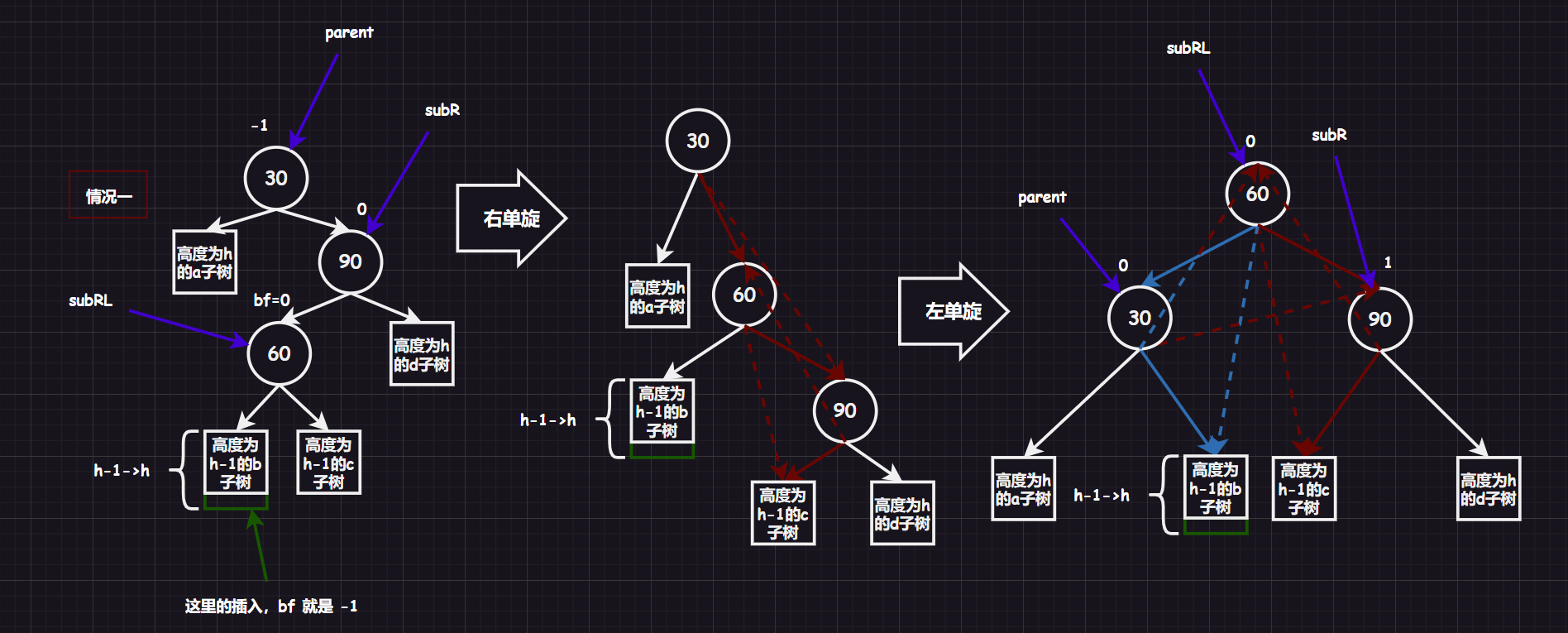
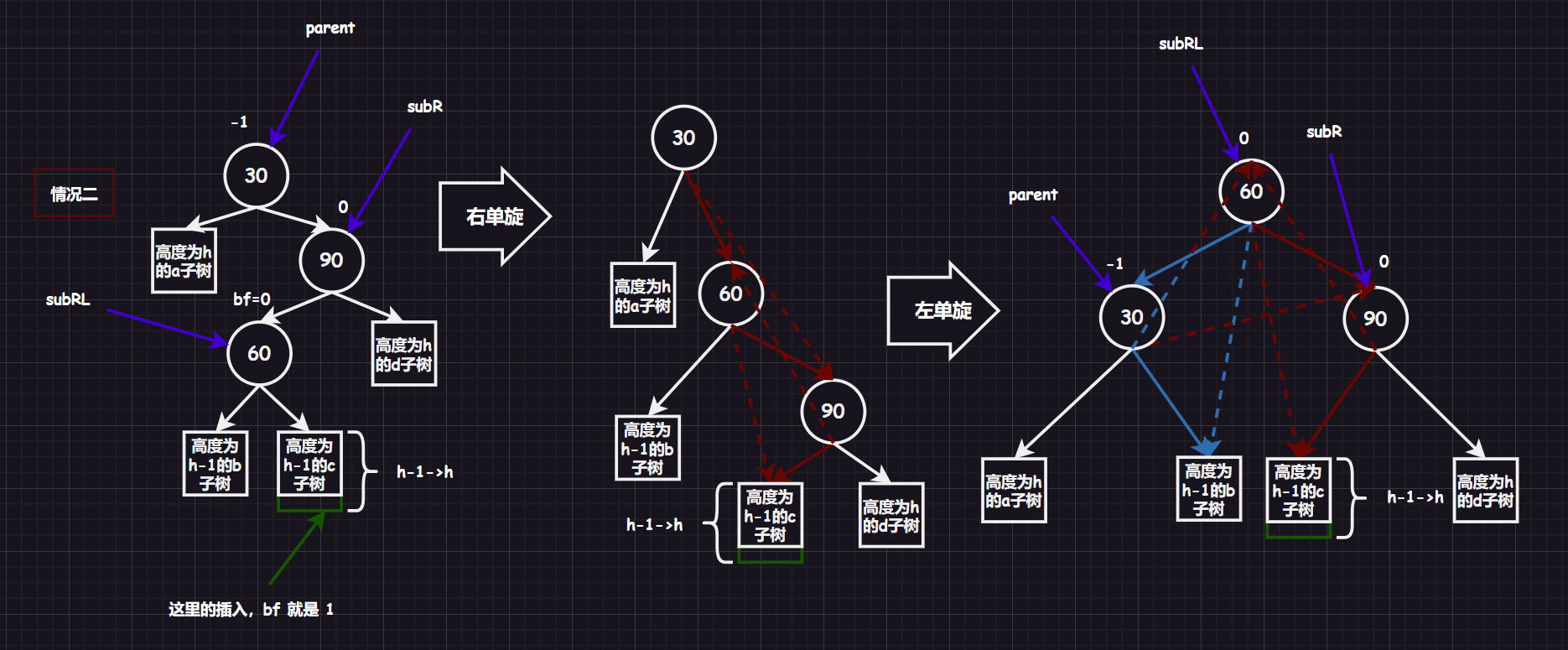
可以看到主要是有两种情况,平衡因子需要特殊设置。
另外最好也要处理一下 h=0 的情况,这种情况就是 b 和 c 子树都不存在,而是插入他们的父节点(在上面例子中就是 60 这个结点),也就是说,插入后 bf=0。
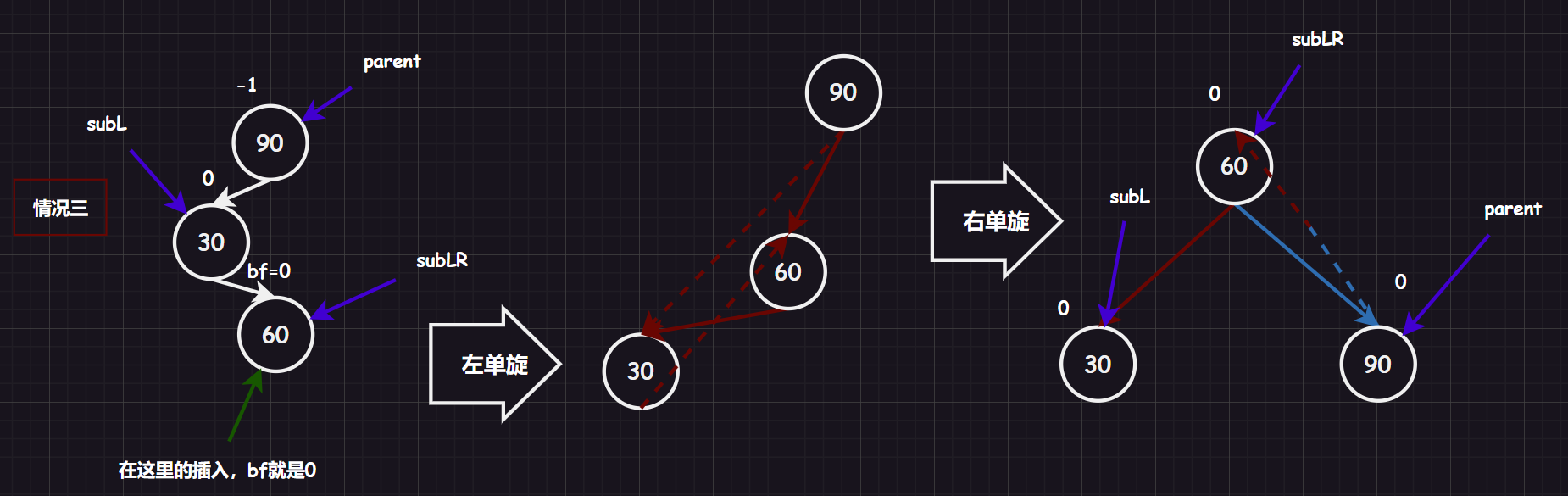
3.2.2.4.先右单旋,再左单旋 [新结点插入较高右子树的左侧]
这个我们也是做抽象树图,不做具体分析(和前一种情况是镜像的)。
然后也要分两种情况:
最好也要处理一下 h=0 的情况:

3.2.3.具体实现
上面我们的抽象树图没有考虑诸多字段/指针(比如父指针、还有根指针),下面我们将上述抽象树图做进一步细化,并且将旋转过程和具体代码一样对应起来。
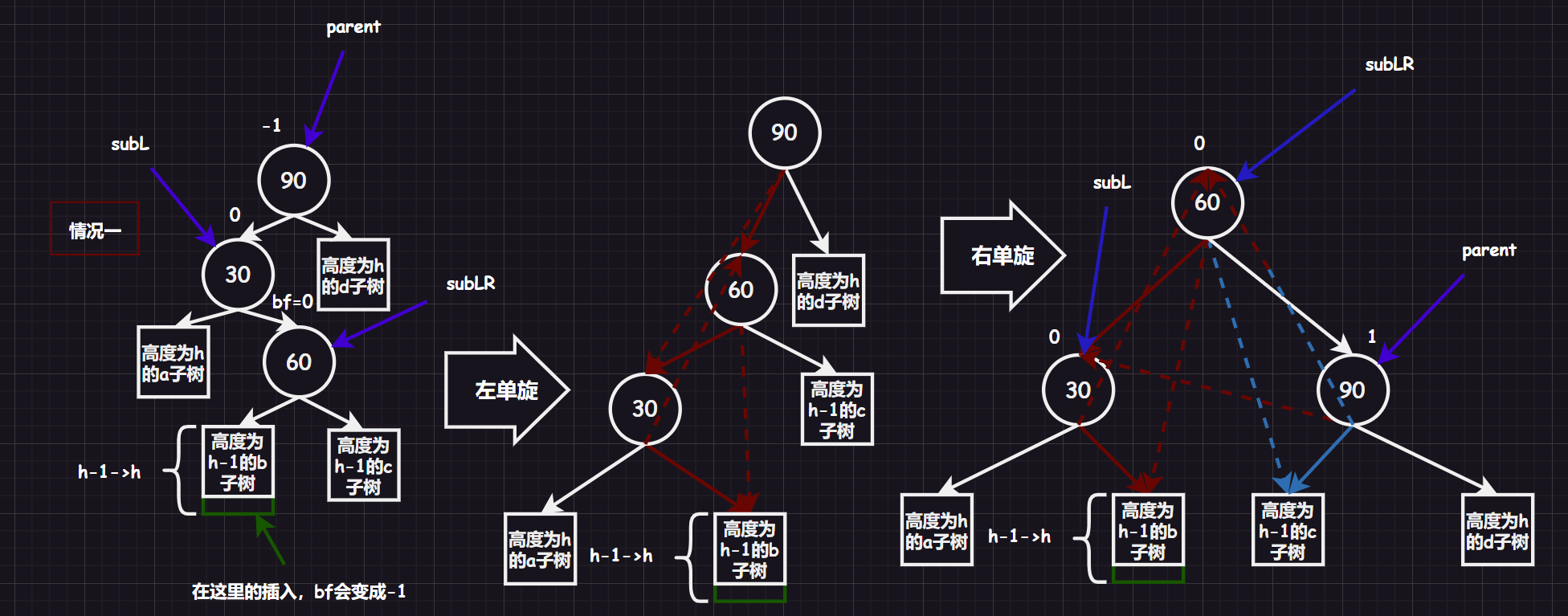
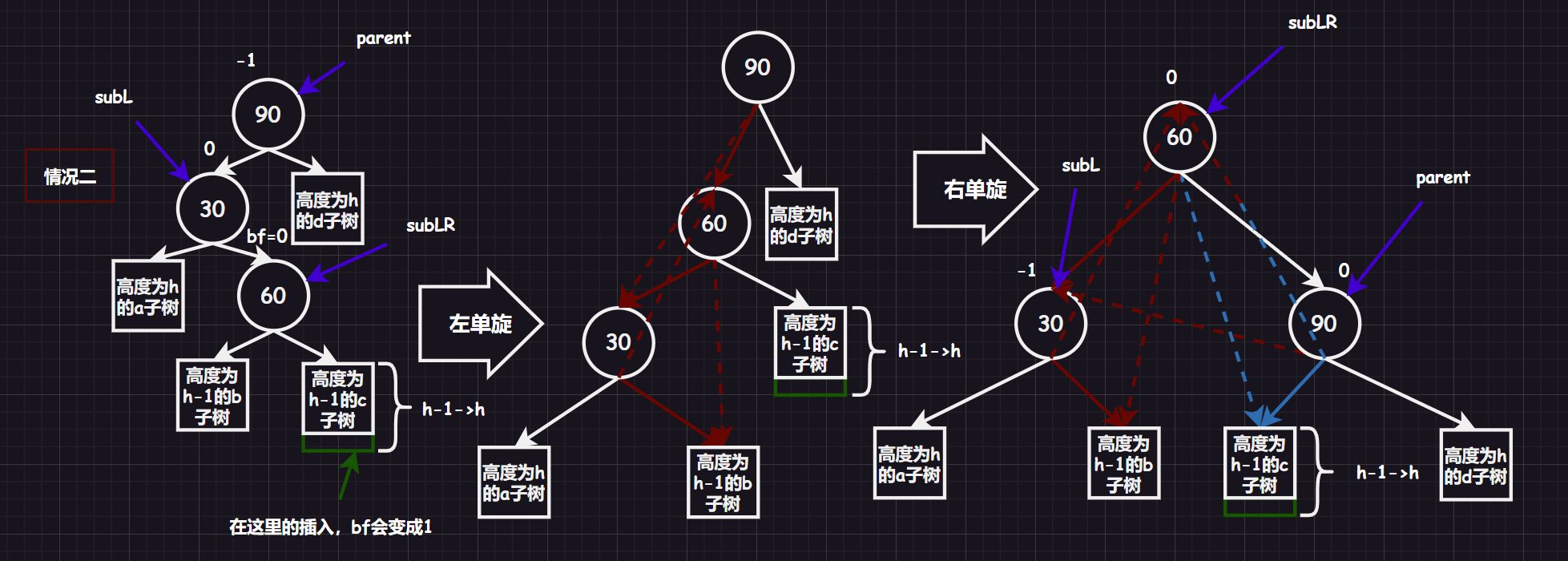
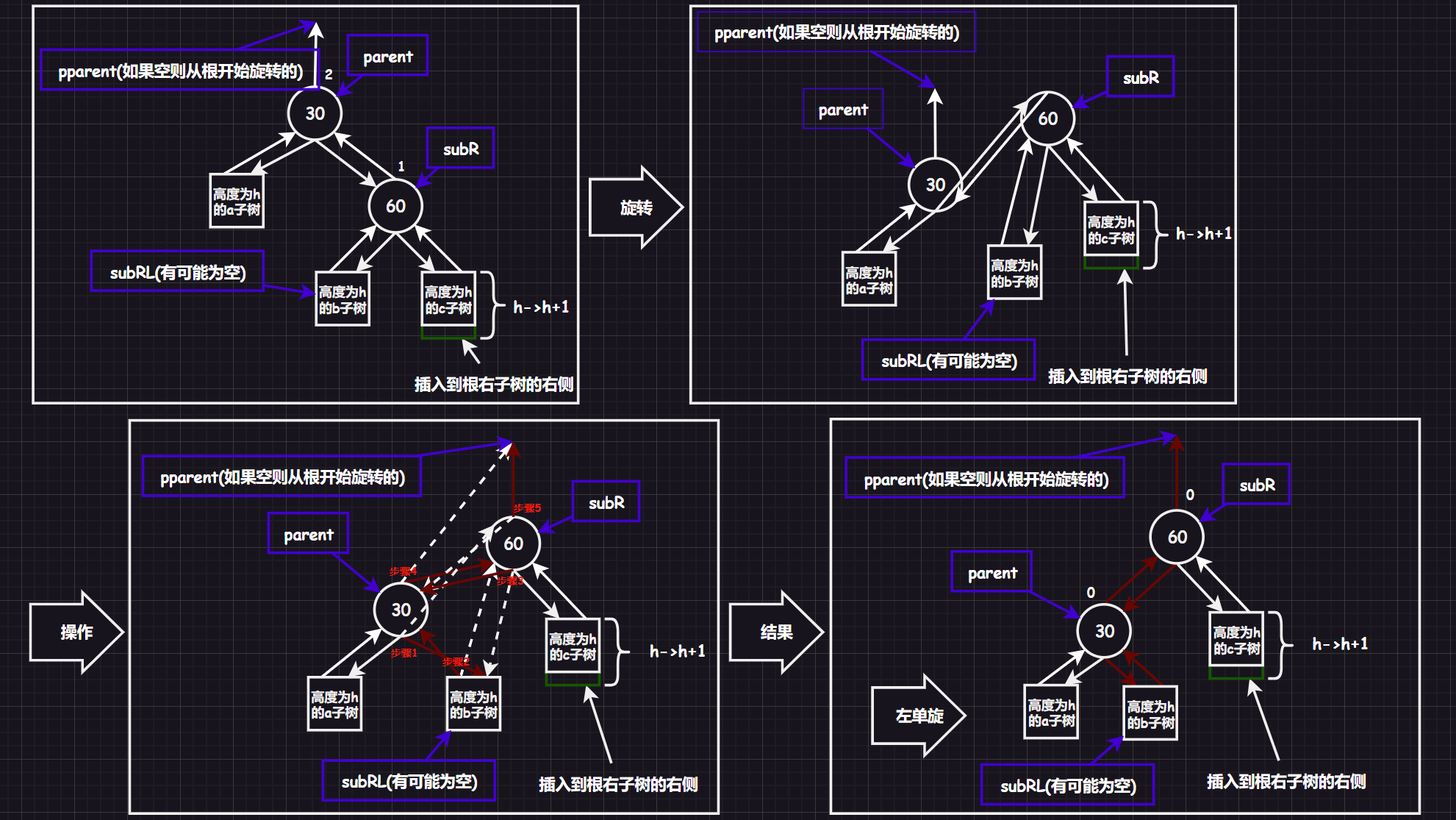
3.2.3.1.左单旋指针图解
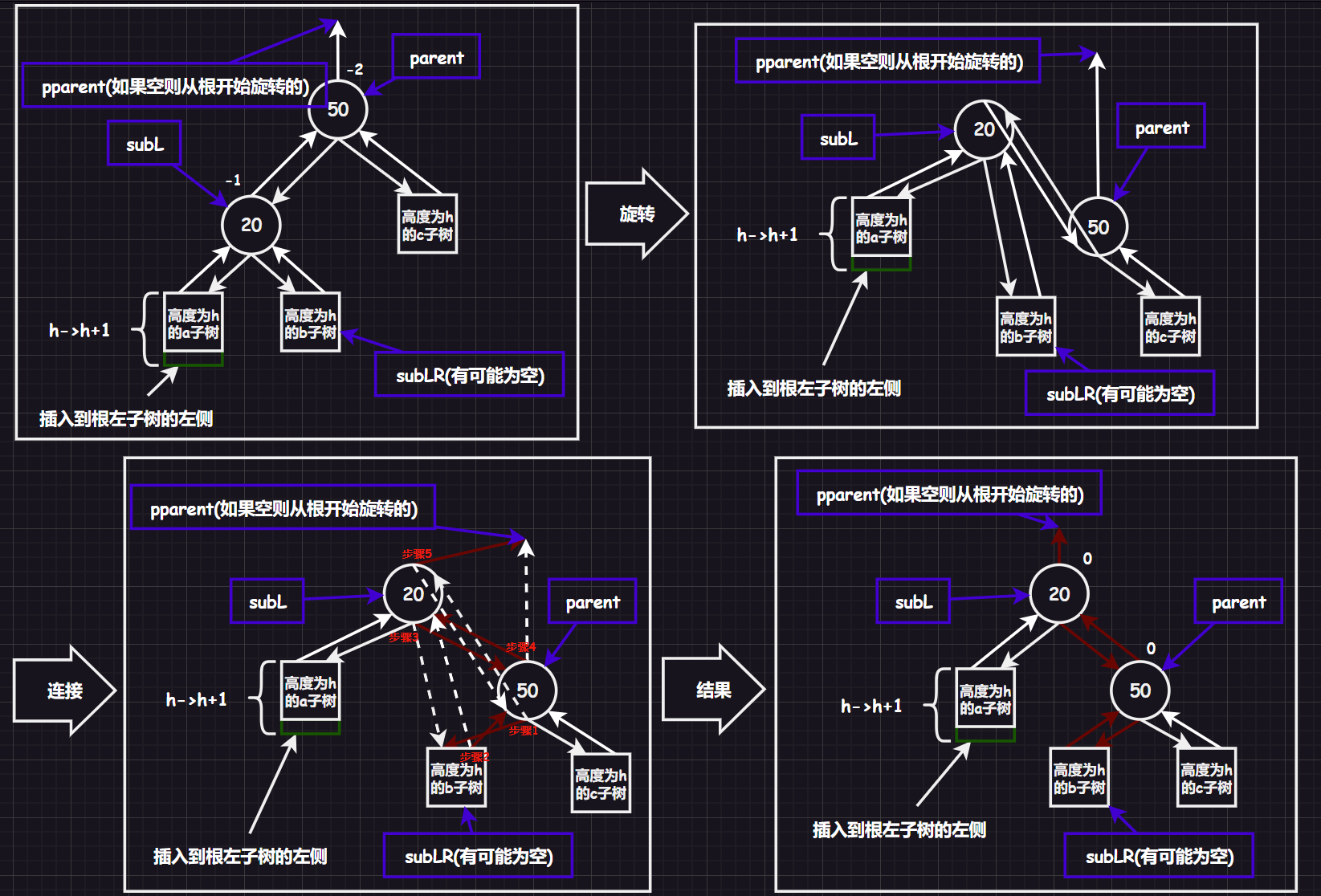
3.2.3.2.右单旋指针图解
3.2.3.3.先左后右指针图解
实际上就是先左单旋,后右单旋,就无须绘图了,只需根据抽象树图来复用前两个函数即可,就是需要注意调整平衡因子。
3.2.3.4.先右后左指针图解
实际上就是先右单旋,后左单旋,就无须绘图了,只需根据抽象树图来复用前两个函数即可,就是需要注意调整平衡因子。
//AVLTree.hpp
//接下来我们来完善一下Insert()的代码,成为完整的插入函数,并且做一次完整的测试
#include <iostream>
#include <utility>
#include <cassert>
using namespace std;
namespace limou
{
//1.结点结构体
template <typename Key, typename Value>
struct AVLTreeNode
{
AVLTreeNode<Key, Value>* _left;
AVLTreeNode<Key, Value>* _right;
AVLTreeNode<Key, Value>* _parent;
pair<Key, Value> _kv;
int _bf;
AVLTreeNode(const pair<Key, Value>& kv)
: _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
, _bf(0)
{}
};
//2.AVLTree类
template <typename Key, typename Value>
class AVLTree
{
typedef AVLTreeNode<Key, Value> Node;
public:
bool Inster(const pair<Key, Value>& kv)
{
//1.搜索二叉树插入的部分
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else//不可以等于
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first > kv.first)
{
parent->_left = cur;
}
else//parent->_kv.first < kv.first)
{
parent->_right = cur;
}
cur->_parent = parent;
//2.AVL的部分开始
//插入cur后,更新结点的父节点平衡因子:
//if(cur == parent->right)
// parent->_bf++
//else(cur == parent->left)
// parent->_bf--
//然后出现以下情况:
//if(parent->_bf == 1 || parent->_bf == -1),
//{
// 说明父结点原本的平衡因子必为 parent->_bf == 0,
// 就说明插入后父节点的左右子树高度差发生了改变,
// 则要向上持续更新父节点的部分/全部祖先平衡因子
// if(cur == parent->right) parent->_bf++
// else(cur == parent->left) parent->_bf--
// ...
//}
//else if(parent->_bf == 2 || parent->_bf == -2)
//{
// 说明父节点所在的左右子树已经不平衡了,需要旋转
//}
//else
//{
// 原本是parent->_bf == 1 or parent->_bf == -1,
// 而新插入的cur把高度低的子树变高了,这说明:
// 父节点的左右子树变成了绝对平衡(平衡因子==0),无需更新祖先
//}
//由于插入结点会影响自己的部分/全部的祖先,因此我们的结构加上_parent指针
//然后需要注意有可能会更新到根结点去(最差情况)
while (parent)//最差更新到根节点,根结点的父节点为空,就可以停下
{
if (cur == parent->_right)
{
parent->_bf++;
}
else//cur == parent->_left
{
parent->_bf--;
}
if (parent->_bf == 1 || parent->_bf == -1)
{
//继续更新
parent = parent->_parent;
cur = cur->_parent;
}
else if (parent->_bf == 0)
{
break;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
//旋转
if (parent->_bf == 2 && cur->_bf == 1)//左单旋
{
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1)//右单旋
{
RotateR(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)//右左双旋
{
RotateLAndR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)//左右双旋
{
RotateRAndL(parent);
}
else
{
assert(false);
}
break;
}
else
{
assert(false);//留给我们自己调试使用
}
}
return true;
}
//2.中序遍历
void InOrder()
{
_InOrder(_root);
std::cout << std::endl;
}
//3.检查是否平衡
bool IsBalance()
{
return _IsBalance(_root);
}
private:
//左单旋
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* pparent = parent->_parent;
//记录了四个指针parent、subR、subRL、pparent
//步骤1
parent->_right = subRL;
//步骤2
if (subRL)//不为空才连接
subRL->_parent = parent;
//步骤3
subR->_left = parent;
//步骤4
parent->_parent = subR;
//步骤5
if (pparent == nullptr)//说明是从根结点开始旋转的
{
_root = subR;//换子
_root->_parent = nullptr;//置空
}
else//如果不是根
{
if (pparent->_left == parent)
{
pparent->_left = subR;//换子
}
else
{
pparent->_right = subR;//换子
}
subR->_parent = pparent;//换父
}
//更新平衡因子
parent->_bf = subR->_bf = 0;
}
//右单旋
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* pparent = parent->_parent;
//记录了四个指针parent、subR、subRL、pparent
//步骤1
parent->_left = subLR;
//步骤2
if (subLR)//不为空才连接
subLR->_parent = parent;
//步骤3
subL->_right = parent;
//步骤4
parent->_parent = subL;
//步骤5
if (pparent == nullptr)//说明是从根结点开始旋转的
{
_root = subL;//换子
_root->_parent = nullptr;//置空
}
else//如果不是根
{
if (pparent->_left == parent)
{
pparent->_left = subL;//换子
}
else
{
pparent->_right = subL;//换子
}
subL->_parent = pparent;//换父
}
//更新平衡因子
parent->_bf = subL->_bf = 0;
}
//双旋:左单旋,右单旋
void RotateLAndR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
//这里的复用代码很简单,但是双旋最困难的问题是更新平衡因子
RotateL(parent->_left);
RotateR(parent);
if (bf == -1)//在较高左子树的右树的右插入
{
parent->_bf = 1;
subLR->_bf = 0;
subL->_bf = 0;
}
else if (bf == 1)//在较高左子树的右树的左插入
{
parent->_bf = 0;
subLR->_bf = 0;
subL->_bf = -1;
}
else if (bf == 0)//建议写上,逻辑更清晰
{
parent->_bf = 0;
subLR->_bf = 0;
subL->_bf = 0;
}
else
{
assert(false);//供自己调试使用
}
}
//双旋:右单旋,左单旋
void RotateRAndL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
//这里的复用代码很简单,但是双旋最困难的问题是更新平衡因子
RotateR(parent->_right);
RotateL(parent);
if (bf == -1)//在较高右子树的左树的左插入
{
parent->_bf = 0;
subRL->_bf = 0;
subR->_bf = 1;
}
else if (bf == 1)//在较高右子树的左树的右插入
{
parent->_bf = -1;
subRL->_bf = 0;
subR->_bf = 0;
}
else if (bf == 0)//建议写上,逻辑更清晰
{
parent->_bf = 0;
subRL->_bf = 0;
subR->_bf = 0;
}
else
{
assert(false);//供自己调试使用
}
}
//中序子函数
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
std::cout << root->_kv.first << "-" << root->_kv.second << " ";
_InOrder(root->_right);
}
//判断平衡的子函数
int _Height(Node* root)
{
if (root == nullptr)
{
return 0;
}
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
bool _IsBalance(Node* root)
{
if (root == nullptr)
{
return true;
}
int leftH = _Height(root->_left);
int rightH = _Height(root->_right);
if (rightH - leftH != root->_bf)//检查平衡因子
{
std::cout << "平衡因子异常:" << root->_kv.first << "-" << root->_kv.second << std::endl;
return false;
}
return abs(leftH - rightH) < 2
&& _IsBalance(root->_left)
&& _IsBalance(root->_right);
}
private:
Node* _root = nullptr;
};
}//测试用例
#include "AVLTree.hpp"
#include <vector>
#include <cstdlib>
#include <ctime>
using namespace std;
#define SIZE 1000000
int main()
{
limou::AVLTree<int, char> a;
//vector<int> arr = { 16,3,7,11,9,26,18,14,15 };
//vector<int> arr = { 4,2,6,1,3,5,15,7,16,14 };
//vector<int> arr = {};
//vector<int> arr = { 1 };
//vector<int> arr = { 1, 2, 3 };
srand((unsigned)time(0));
vector<int> arr;
for (int i = 0; i < SIZE; i++)
{
arr.push_back(rand() % SIZE);
}
for (auto it : arr)
{
a.Inster(make_pair(it, 'a' + (it % 26)));
}
a.InOrder();
if (a.IsBalance())
{
cout << "OK" << endl;
}
return 0;
}而其他的接口,比如:删除,从保持平衡上来看,和普通的二叉搜索树是一样的,就是需要注意平衡因子的问题,但是删除实际上比插入还要复杂,这里挖一个坑以后再来实现。
简单提一下,删除和插入有些地方是相反操作,删除也会导致高度变化,这里推荐看书《数据结构-用面向对象方法与 C++ 描述》殷人昆版,使用细节的实际代码)。
查找就不提了和普通的二叉搜索树是一样的实现。
3.3.性能
AVL 树是绝对平衡的二叉搜索树,这可以保证高效率的查找(即:O(log2(n)),在 10 亿数据的结点下,只需要查找 26 次左右)。但是 AVL 树也有一些缺点:在数据改动较大的动态场景里,频繁的结构修改(插入或者删除)会导致性能非常低下。
4.RB 树
4.1.定义
只需要满足下面的性质即可:
- 在每一个结点内增加一个存储颜色的字段(存储
Red和Black),保证每个结点不是红色就是黑色 - 根节点、空叶子结点(也叫
NIL结点)必须是黑色的 - 如果节点是红色的,则它的两个孩子结点是黑色的(但是对于黑色节点没有规定)
- 对于每个结点,从该结点到其所有后代空叶子结点的路径上,均包含相同数目的黑色结点
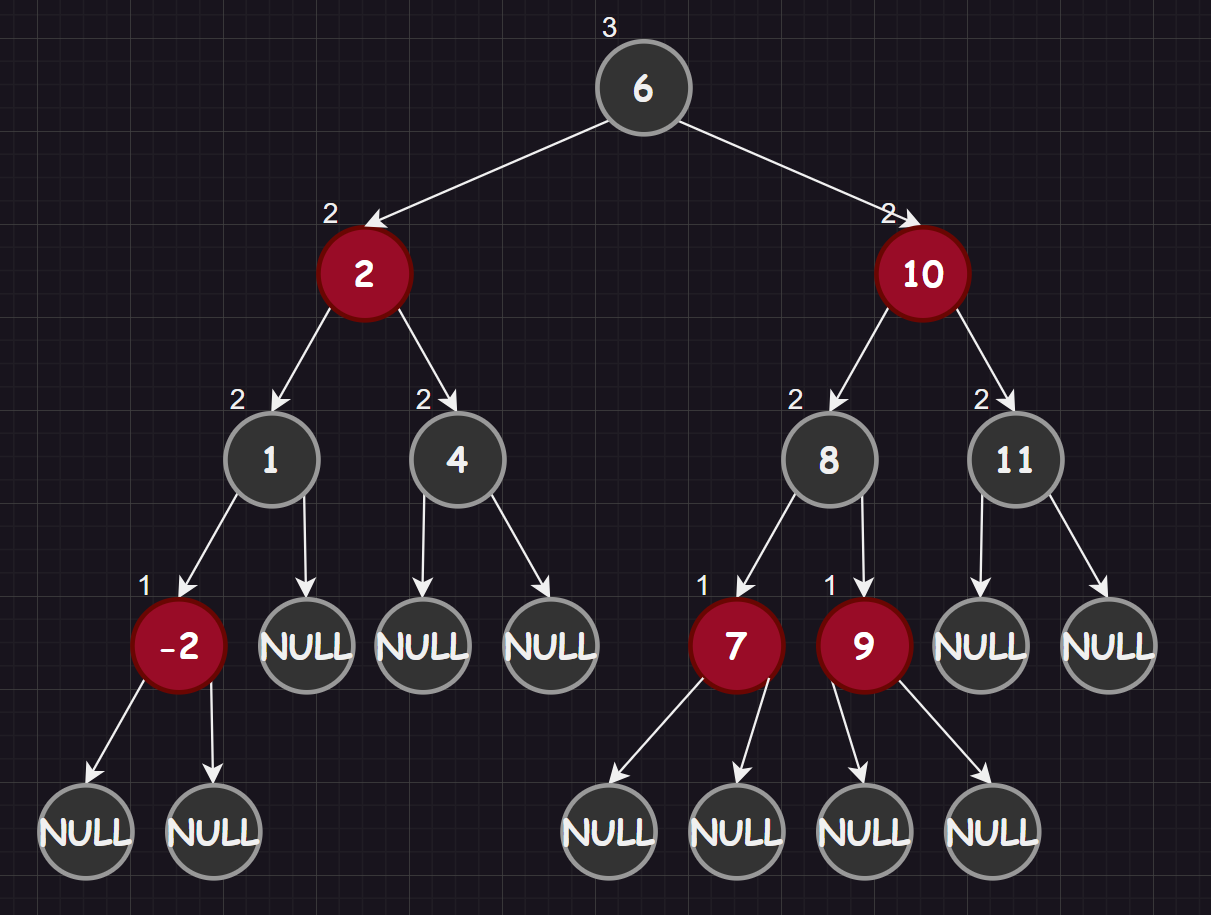
红黑树保证没有一条路径(包括空叶子结点)会比其他路径长两倍,因此是近似平衡,而不是 AVL 树的那种绝对平衡。
不过上述保证的原理是什么呢?这是因为:最 Min 的路径就是全黑路径,最 Max 路径就是红黑间隔路径(当然,实际的红黑树不一定有最短和最长路径)。
这样最长和最短之间为了保证黑结点数量相同,就必须满足红黑间隔路径结点个数是全黑路径结点的两倍。
补充:假设红黑树全部有
N个黑色结点,则最Min路径长度为 log2(N),最Max路径长度为 2log2(N),整棵树的结点个数为 [N,2N]。
RB 树比 AVL 树的查找略差一些,但是对于 CPU 来说差别不大,并且不严格使得 RB 树不至于一直处于旋转的状态,消耗较低。
而后续具体实现的大致框架和 AVL 树差不多,也是重点讲解插入的过程。
4.2.插入
4.2.1.插入结点
插入的大逻辑还是二叉搜索树(但是需要设置颜色)。
4.2.2.设置颜色
如果是插入第一个结点,也就是根结点,那么就设置为黑色即可,而如果不是根结点,最好还是默认插入红色结点(这一默认行为可以直接在 RBTreeNode{/*...*/}; 内的构造函数里实现)。
因为如果是黑色,就会必定违反上述第 4 条规则。如果是红色,就有可能违反第 3 规则。
对比起来违反规则 3 是有可能的,但是总比一定违法规则 4 要更好。
接下来,如果插入红结点:
若其父节点是黑结点,那么插入是不会影响红黑树的性质的
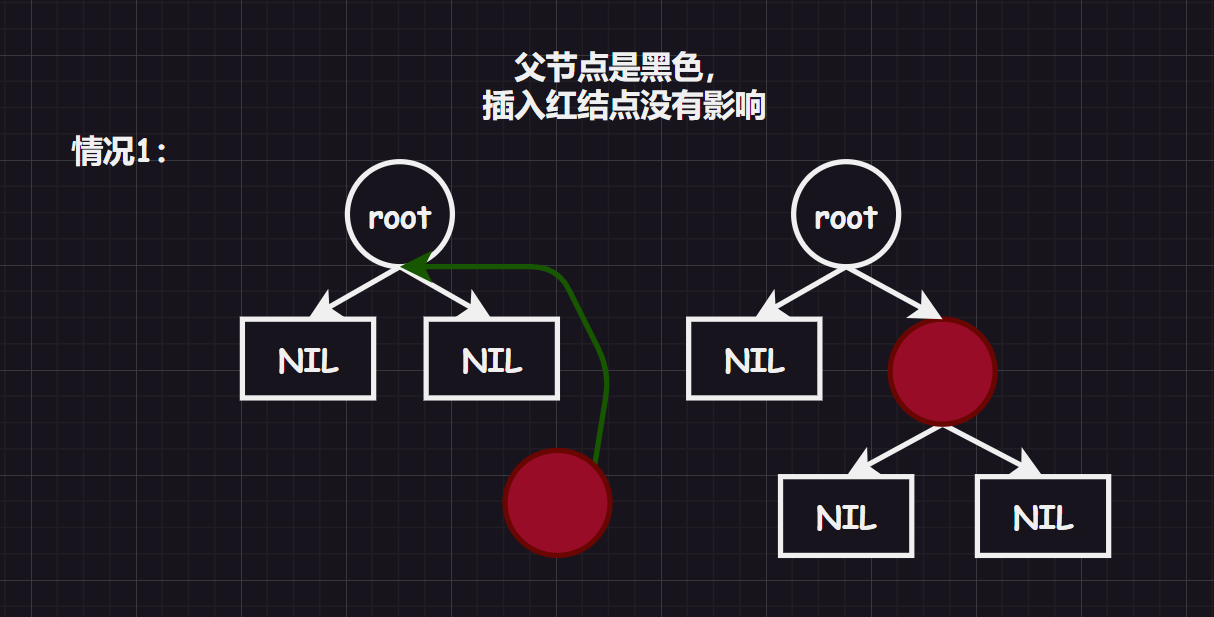
image-20231028113449554 若其父节点是红结点,那么插入就有可能会发生影响,会衍生出两种情况
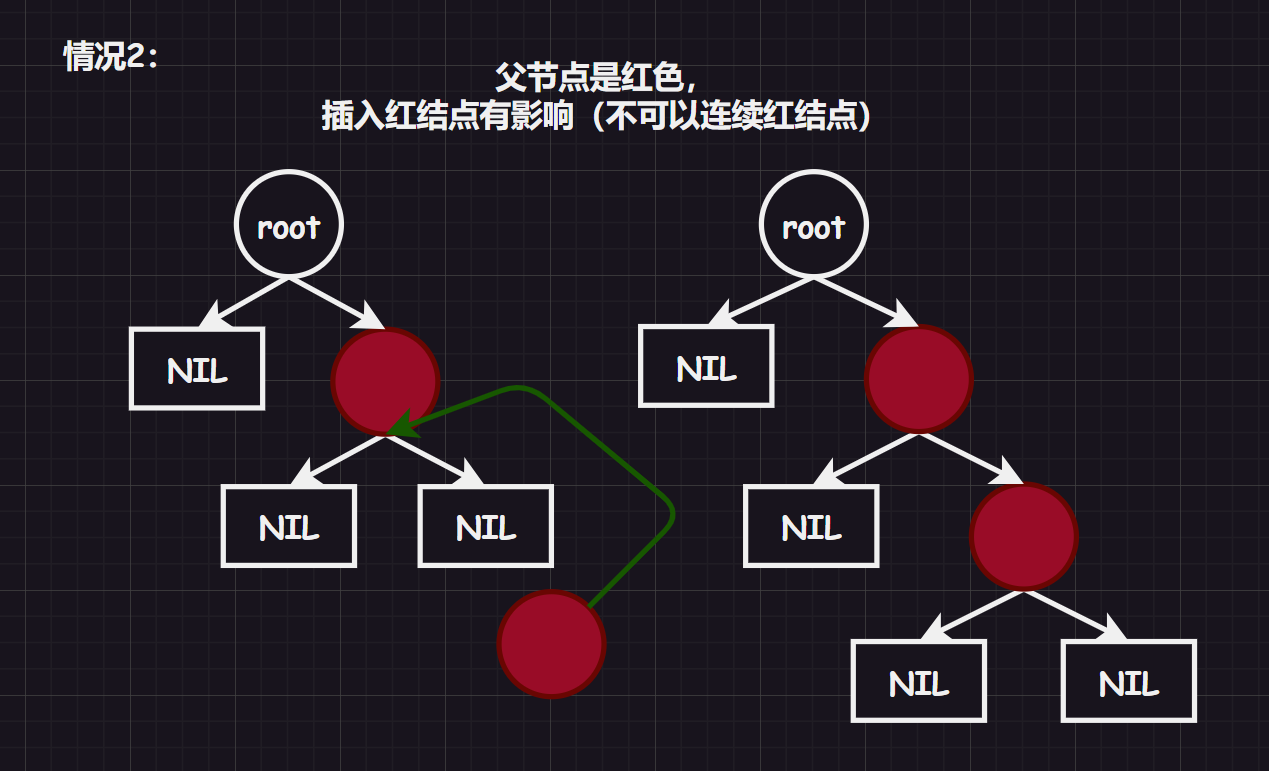
image-20231028113514490
4.2.3.调整结点
针对第二种情况,我们来做细致的分析:
uncle存在且为红uncle不存在或者存在且为黑
4.2.4.具体实现
//AVLTree.hpp
#pragma once
#include <iostream>
#include <utility>
#include <cassert>
#include <cstdio>
#include <cstdlib>
#include <ctime>
namespace limou
{
//1.颜色结构体
enum Colour
{
RED,
BLACK
};
//2.结点结构体
template <typename K, class V>
struct RBTreeNode
{
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
std::pair<K, V> _kv;
Colour _col;
RBTreeNode(const std::pair<K, V>& kv)
: _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
, _col(RED)
{}
};
//3.RBTree类结构
template <typename K, class V>
class RBTree
{
typedef RBTreeNode<K, V> Node;
public://3.1.成员函数
~RBTree()
{
Destroy(_root);
_root = nullptr;
}
bool Insert(const std::pair<K, V>& kv)
{
//1.搜索二叉树插入的部分
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else//不可以等于
{
return false;
}
}
cur = new Node(kv);//默认新增加的是红色结点(这么设置会好一些,这个默认设置行为在RBTreeNode的构造函数里)
if (parent->_kv.first > kv.first)
{
parent->_left = cur;
}
else//parent->_kv.first < kv.first
{
parent->_right = cur;
}
cur->_parent = parent;
//2.RBTree的部分开始
while (parent && parent->_col == RED)//只要父节点为空(避免是根节点)或者父节点是黑(黑就随便插入,不影响RB定义)
{
Node* grandFather = parent->_parent;//parent是红的,就一定存在grandFather(只有parent为根节点才不会有grandFather)
//根据 uncle 的位置来做类似的处理
if (grandFather->_left == parent)
{
Node* uncle = grandFather->_right;
//情况一:uncle 存在并且颜色为红
if (uncle && uncle->_col == RED)
{
parent->_col = BLACK;//设置颜色
uncle->_col = BLACK;
grandFather->_col = RED;
cur = grandFather;//继续往上调整
parent = cur->_parent;
}
else//情况二:uncle 不存在或者颜色为黑
{
if (cur == parent->_left)
{
// g
// p u
// c
RotateR(grandFather);
parent->_col = BLACK;
grandFather->_col = RED;
}
else
{
// g
// p u
// c
RotateL(parent);
RotateR(grandFather);
cur->_col = BLACK;
//parent->_col = RED;//这句话可以不写
grandFather->_col = RED;
}
break;
}
}
else//grandFather->_right == parent
{
Node* uncle = grandFather->_left;
//情况一:uncle 存在并且颜色为红
if (uncle && uncle->_col == RED)
{
parent->_col = BLACK;//设置颜色
uncle->_col = BLACK;
grandFather->_col = RED;
cur = grandFather;//继续往上调整
parent = cur->_parent;
}
else//情况二:uncle 不存在或者颜色为黑
{
if (cur == parent->_right)
{
// g
// u p
// c
RotateL(grandFather);
parent->_col = BLACK;
grandFather->_col = RED;
}
else
{
// g
// u p
// c
RotateR(parent);
RotateL(grandFather);
cur->_col = BLACK;
//parent->_col = RED;//这句话可以不写
grandFather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return true;
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < key)
{
cur = cur->_right;
}
else if (cur->_kv.first > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
private://3.2.辅助函数
//左单旋
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* pparent = parent->_parent;
//记录了四个指针parent、subR、subRL、pparent
//步骤1
parent->_right = subRL;
//步骤2
if (subRL)//不为空才连接
subRL->_parent = parent;
//步骤3
subR->_left = parent;
//步骤4
parent->_parent = subR;
//步骤5
if (pparent == nullptr)//说明是从根结点开始旋转的
{
_root = subR;//换子
_root->_parent = nullptr;//置空
}
else//如果不是根
{
if (pparent->_left == parent)
{
pparent->_left = subR;//换子
}
else
{
pparent->_right = subR;//换子
}
subR->_parent = pparent;//换父
}
//无需更新平衡因子(RBTree没有这个东西)
//parent->_bf = subR->_bf = 0;
}
//右单旋
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* pparent = parent->_parent;
//记录了四个指针parent、subR、subRL、pparent
//步骤1
parent->_left = subLR;
//步骤2
if (subLR)//不为空才连接
subLR->_parent = parent;
//步骤3
subL->_right = parent;
//步骤4
parent->_parent = subL;
//步骤5
if (pparent == nullptr)//说明是从根结点开始旋转的
{
_root = subL;//换子
_root->_parent = nullptr;//置空
}
else//如果不是根
{
if (pparent->_left == parent)
{
pparent->_left = subL;//换子
}
else
{
pparent->_right = subL;//换子
}
subL->_parent = pparent;//换父
}
//无需更新平衡因子(RBTree没有这个东西)
//parent->_bf = subL->_bf = 0;
}
//销毁
void Destroy(Node* root)
{
if (root == nullptr)
{
return;
}
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
private://3.3.测试函数
//检查性质(辅助测试)
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
std::cout << root->_kv.first << " ";
_InOrder(root->_right);
}
//检查颜色(辅助测试)
bool _Check(Node* root, int blackNum, int benchmark)
{
if (root == nullptr)
{
//走到空的时候就检查黑色结点的数量和是否相等(没有记录黑结点)
if (benchmark != blackNum)
{
std::cout << "某条路径黑色节点的数量不相等,违反:4.对于每个结点,从该结点到其所有后代空叶子结点的路径上,均包含相同数目的黑色结点" << std::endl;
return false;
}
return true;
}
if (root->_col == BLACK)
{
++blackNum;
}
if (root->_col == RED
&& root->_parent
&& root->_parent->_col == RED)//这里倒过来检查,如果检查父节点的子,有可能出现空的情况
{
std::cout << "存在连续的红色节点,违反:3.如果一个节点是红色的,则它的两个孩子结点是黑色的" << std::endl;
return false;
}
return _Check(root->_left, blackNum, benchmark)
&& _Check(root->_right, blackNum, benchmark);
}
//检查高度(辅助测试)
int _Height(Node* root)
{
if (root == NULL)
return 0;
int leftH = _Height(root->_left);
int rightH = _Height(root->_right);
return leftH > rightH ? leftH + 1 : rightH + 1;
}
public:
void InOrder()
{
_InOrder(_root);
std::cout << std::endl;
}
bool IsBalance()
{
//根据红黑树的定义来检查
//1.在每一个结点内增加一个存储颜色的字段(存储 Red 和 Black),保证每个结点不是红色就是黑色(这点可以不证明)
//2.根节点、空叶子结点(也叫 NIL 结点)必须是黑色的
if (_root && _root->_col == RED)
{
std::cout << "违反:2.根节点、空叶子结点(也叫 NIL 结点)必须是黑色的" << std::endl;
return false;
}
//3.如果一个节点是红色的,则它的两个孩子结点是黑色的
//4.对于每个结点,从该结点到其所有后代空叶子结点的路径上,均包含相同数目的黑色结点
int benchmark = 0;//一个基准值
Node* cur = _root;
while (cur)//先走一条路,得出黑色结点的数量,然后检查每一条路径就可以了(没有记录黑空结点)
{
if (cur->_col == BLACK)
++benchmark;
cur = cur->_left;
}
return _Check(_root, 0, benchmark);//检查是否有连续红色节点
}
int Height()
{
return _Height(_root);
}
private://3.4.成员变量
Node* _root = nullptr;
};
//4.测试函数(证明符合RB二叉搜索树)
//4.1.证明一(有限证明)
void Test_1_RBTree()
{
int arr[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
RBTree<int, int> r;
for (auto e : arr)
{
r.Insert(std::make_pair(e, e));
}
r.InOrder();
r.IsBalance();
std::cout << "高度:" << r.Height() << std::endl;
}
//4.2.证明二(随机证明)
void Test_2_RBTree()
{
//设置要插入的数量
int size = 100000;
//设置随机数
srand(time(0));
//开始插入验证
RBTree<int, int> r;
while (size--)
{
int x = rand();
r.Insert(std::make_pair(x, x));
}
r.InOrder();
r.IsBalance();
std::cout << "高度:" << r.Height() << std::endl;
}
}4.3.性能
5.set 和 map 的实现
下面我们就利用我们已有的红黑树简单封装出一个 set 和 map,
5.1.红黑树模板
以下是红黑树类模板的部分代码,这里忽略了很多代码:
//RBTree.hpp
template <class Value>
struct __rb_tree_node : public __rb_tree_node_base
{
typedef __rb_tree_node<Value>* link_type;
Value value_field;
};
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc = alloc>
class rb_tree
{
typedef __rb_tree_node<Value> rb_tree_node;
typedef rb_tree_node* link_type;
size_type node_count;
link_type header;
};5.2.封装 set 和 map
此时就可以使用红黑树类模板来封装出 set 和 map,使用 set<K, K> 和 map<K, V>。其中,第一个模板参数用来记忆 K 的类型,不然没办法正确构造出 find() 和 erase() 接口,第二个模板参数就决定树节点存储的类型。
5.3.自定义封装
接下来我们根据之前实现的红黑树代码,来封装出 set 和 map 容器。
//RBTree.hpp
#pragma once
/* ---在很多库中的实现---
template <class Value>
struct __rb_tree_node : public __rb_tree_node_base
{
typedef __rb_tree_node<Value>* link_type;
Value value_field;
};
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc = alloc>
class rb_tree
{
typedef __rb_tree_node<Value> rb_tree_node;
typedef rb_tree_node* link_type;
size_type node_count;
link_type header;
};
*/
#include <iostream>
#include <string>
#include <vector>
#include <utility>
#include <cassert>
#include <cstdio>
#include <cstdlib>
#include <ctime>
namespace limou
{
//1.颜色结构体
enum Colour
{
RED,
BLACK
};
//2.结点结构体
template <class T>
struct RBTreeNode
{
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;
Colour _col;
RBTreeNode(const T& data)
: _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
, _col(RED)
{}
};
//3.迭代器类结构(用结点去构造一个迭代器然后返回)
template<class T, class Ref, class Ptr>
struct __RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef __RBTreeIterator<T, Ref, Ptr> Self;
Node* _node;
__RBTreeIterator(Node* node) : _node(node) {}
__RBTreeIterator(const __RBTreeIterator<T, T&, T*>& it) : _node(it._node) {}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &_node->_data;
}
bool operator!=(const Self& s)
{
return _node != s._node;
}
Self& operator++()
{
if (_node->_right != nullptr)
{
//右不空,就找右子树的最左结点
Node* subLeft = _node->_right;
while (subLeft->_left)
{
subLeft = subLeft->_left;
}
_node = subLeft;
}
else
{
//右为空,说明要重新走一次中序遍历(前面左子树和根一点遍历过了),
//沿着根结点路径,选择祖先(从祖先路径中选择将自己视为左子树的第一个祖先结点),
//如果没有可以选择的祖先,直接设置为空,代表遍历结束
//由于我们有三叉链,实现起来比较简单(如果没有设计这种结构,也可以使用栈结构辅助)
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_right)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Self& operator--()
{
//走右根左,和 ++ 相反即可
if (_node->_left != nullptr)
{
//左不空,就找左子树的最右结点
Node* subRight = _node->_left;
while (subRight->_right)
{
subRight = subRight->_right;
}
_node = subRight;
}
else
{
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_left)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
};
//4.RBTree类结构
template <typename K, class T, class KeyOfT>
class RBTree
{
public://迭代器
typedef RBTreeNode<T> Node;
typedef __RBTreeIterator<T, T&, T*> iterator;
typedef __RBTreeIterator<T, const T&, const T*> const_iterator;
iterator begin()
{
Node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return iterator(cur);
}
iterator end()
{
return iterator(nullptr);
}
const_iterator begin() const
{
Node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return const_iterator(cur);
}
const_iterator end() const
{
return const_iterator(nullptr);
}
public://成员函数
~RBTree()
{
Destroy(_root);
_root = nullptr;
}
/*
下面的 data 已经是泛型了,有可能是 Key,也有可能是 Key-Value
后者虽然可以直接比较大小,但是不是我们想要的,
其底层比较的是先比较 key 再比较 value。
而我们只期望比较 key 的值,为了解决这个问题,
我们采用仿函数来对这种泛型进行比较
*/
std::pair<iterator, bool> Insert(const T& data)
{
//1.搜索二叉树插入的部分
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
return std::make_pair(iterator(_root), true);
}
KeyOfT kot;
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (kot(cur->_data) < kot(data))
{
parent = cur;
cur = cur->_right;
}
else if (kot(cur->_data) > kot(data))
{
parent = cur;
cur = cur->_left;
}
else//不可以等于
{
return std::make_pair(iterator(cur), false);
}
}
cur = new Node(data);//默认新增加的是红色结点(这么设置会好一些,这个默认设置行为在RBTreeNode的构造函数里)
Node* copy = cur;
if (kot(parent->_data) > kot(data))
{
parent->_left = cur;
}
else//parent->_kv.first < kv.first
{
parent->_right = cur;
}
cur->_parent = parent;
//2.RBTree的部分开始
while (parent && parent->_col == RED)//只要父节点为空(避免是根节点)或者父节点是黑(黑就随便插入,不影响 RB 定义)
{
Node* grandFather = parent->_parent;//parent 是红的,就一定存在 grandFather(只有 parent 为根节点才不会有 grandFather)
//根据 uncle 的位置来做类似的处理
if (grandFather->_left == parent)
{
Node* uncle = grandFather->_right;
//情况一:uncle 存在并且颜色为红
if (uncle && uncle->_col == RED)
{
parent->_col = BLACK;//设置颜色
uncle->_col = BLACK;
grandFather->_col = RED;
cur = grandFather;//继续往上调整
parent = cur->_parent;
}
else//情况二:uncle 不存在或者颜色为黑
{
if (cur == parent->_left)
{
// g
// p u
// c
RotateR(grandFather);
parent->_col = BLACK;
grandFather->_col = RED;
}
else
{
// g
// p u
// c
RotateL(parent);
RotateR(grandFather);
cur->_col = BLACK;
//parent->_col = RED;//这句话可以不写
grandFather->_col = RED;
}
break;
}
}
else//grandFather->_right == parent
{
Node* uncle = grandFather->_left;
//情况一:uncle 存在并且颜色为红
if (uncle && uncle->_col == RED)
{
parent->_col = BLACK;//设置颜色
uncle->_col = BLACK;
grandFather->_col = RED;
cur = grandFather;//继续往上调整
parent = cur->_parent;
}
else//情况二:uncle 不存在或者颜色为黑
{
if (cur == parent->_right)
{
// g
// u p
// c
RotateL(grandFather);
parent->_col = BLACK;
grandFather->_col = RED;
}
else
{
// g
// u p
// c
RotateR(parent);
RotateL(grandFather);
cur->_col = BLACK;
//parent->_col = RED;//这句话可以不写
grandFather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return std::make_pair(copy, true);
}
Node* Find(const K& key)
{
Node* cur = _root;
KeyOfT kot;
while (cur)
{
if (kot(cur->_data) < key)
{
cur = cur->_right;
}
else if (kot(cur->_data) > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
private://辅助函数
//左单旋
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* pparent = parent->_parent;
//记录了四个指针parent、subR、subRL、pparent
//步骤1
parent->_right = subRL;
//步骤2
if (subRL)//不为空才连接
subRL->_parent = parent;
//步骤3
subR->_left = parent;
//步骤4
parent->_parent = subR;
//步骤5
if (pparent == nullptr)//说明是从根结点开始旋转的
{
_root = subR;//换子
_root->_parent = nullptr;//置空
}
else//如果不是根
{
if (pparent->_left == parent)
{
pparent->_left = subR;//换子
}
else
{
pparent->_right = subR;//换子
}
subR->_parent = pparent;//换父
}
//无需更新平衡因子(RBTree没有这个东西)
//parent->_bf = subR->_bf = 0;
}
//右单旋
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* pparent = parent->_parent;
//记录了四个指针parent、subR、subRL、pparent
//步骤1
parent->_left = subLR;
//步骤2
if (subLR)//不为空才连接
subLR->_parent = parent;
//步骤3
subL->_right = parent;
//步骤4
parent->_parent = subL;
//步骤5
if (pparent == nullptr)//说明是从根结点开始旋转的
{
_root = subL;//换子
_root->_parent = nullptr;//置空
}
else//如果不是根
{
if (pparent->_left == parent)
{
pparent->_left = subL;//换子
}
else
{
pparent->_right = subL;//换子
}
subL->_parent = pparent;//换父
}
//无需更新平衡因子(RBTree没有这个东西)
//parent->_bf = subL->_bf = 0;
}
//销毁
void Destroy(Node* root)
{
if (root == nullptr)
{
return;
}
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
private://成员变量
Node* _root = nullptr;
};
}//Set.hpp
#pragma once
#include "RBTree.hpp"
namespace limou
{
template<class K>
class Set
{
private://内部类(泛函数)
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;//可以取出 key,这是为了和 map 同步
}
};
public://迭代器
//这里的 iterator 实际上也是常量迭代器,由于 set 容器为了满足二叉搜索性质,
//不能改动 key,而我们设计的迭代器器会返回可以修改的迭代器,一旦允许改动,
//就会出现 bug,因此干脆返回一个常量迭代器,伪装成普通迭代器
typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;
//注意获取别的类的内嵌类型需要用到 typename(不然无法区分是静态成员还是类型)
typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;
iterator begin()
{
//一旦上述普通迭代器成为常量迭代器的伪装,
//这里调用的还是普通迭代器 begin(),
//无法转为常量迭代器来作为函数返回值返回,
//因此就需要将普通迭代器转化为常量迭代器
//转化方法就是在 __RBTreeIterator 中,
//多写一个用于转化的构造函数
return _t.begin();
}
iterator end()
{
return _t.end();
}
public://成员函数
std::pair<iterator, bool> Insert(const K& key)
{
return _t.Insert(key);
}
private://成员变量
RBTree<K, K, SetKeyOfT> _t;
};
//测试函数
void test_set()
{
Set<int> s;
s.Insert(3);
s.Insert(1);
s.Insert(2);
s.Insert(10);
s.Insert(4);
s.Insert(100);
s.Insert(5);
for (auto e : s)
{
std::cout << e << " ";
}
std::cout << std::endl;
}
}//Map.hpp
#pragma once
#include "RBTree.hpp"
namespace limou
{
template<class K, class V>
class Map
{
private://内部类(泛函数)
struct MapKeyOfT
{
const K& operator()(const std::pair<const K, V>& kv)
{
return kv.first;//可以取出 key 的部分
}
};
public://迭代器
typedef typename RBTree<K, std::pair<const K, V>, MapKeyOfT>::iterator iterator;//获取别的类的内嵌类型需要用到typename(不然无法区分是静态成员还是类型)
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
public://成员函数
std::pair<iterator, bool> Insert(const std::pair<const K, V>& kv)
{
return _t.Insert(kv);
}
V& operator[](const K& key)
{
std::pair<iterator, bool> ret = _t.Insert(std::make_pair(key, V()));
return ret.first->second;
}
private://成员变量
RBTree<K, std::pair<const K, V>, MapKeyOfT> _t;
};
//测试函数
void test_map()
{
Map<int, int> m1;
m1.Insert(std::make_pair(1, 1));
m1.Insert(std::make_pair(3, 1));
m1.Insert(std::make_pair(4, 1));
m1.Insert(std::make_pair(2, 1));
m1.Insert(std::make_pair(10, 1));
m1.Insert(std::make_pair(50, 1));
m1.Insert(std::make_pair(0, 1));
for (auto e : m1)
{
std::cout << "<" << e.first << "," << e.second << ">" << " ";
}
std::cout << std::endl;
Map<std::string, int> m2;
std::vector<std::string> arr = { "红色", "白色", "绿色", "红色", "黑色", "黑色", "红色", "红色" };
for (auto e : arr)
{
m2[e]++;
}
for (auto e : m2)
{
std::cout << "<" << e.first << "," << e.second << ">" << std::endl;
}
}
}更新日志
403d4-修改 Github 工作流的配置,以方便未来支持前后端拓展于